Fuzzy Clustering

Contents

Fuzzy Clustering#

In crisp clustering a sample can only belong to one cluster whereas in fuzzy clustering a sample is assigned to all clusters but it has probability assigned to it of belonging to a certain cluster (Paasche and Eberle, 2009, 2011). This is referred to as the membership of a sample to a cluster. Higher membership means the sample is closer to the centre of the cluster (Paasche and Eberle, 2009). If a sample falls in between two classes, it may have a 50% probability that it belongs to either of the two classes. There are different ways of defining the classes that are similar to crisp clustering, e.g. fuzzy C-means, advanced fuzzy C-means and Gustafson Kessel. The figure below illustrates the relation between the crisp clustering algorithms and the fuzzy clustering algorithms.

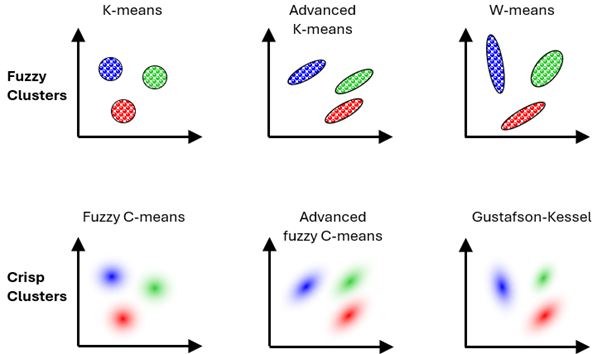
_images/clustfuzzy1.png

Simple illustration comparing crisp and fuzzy clustering algorithms.#

The Fuzzy Clustering interface has the following options:

  1. Cluster Algorithm – This can be fuzzy c-means, advanced fuzzy c-means or Gustafson-Kessel

  2. Minimum Clusters – Clustering can be done for a specific number of clusters or for a range of clusters. This option sets the minimum number of clusters that will be generated.

  3. Maximum Clusters – The maximum number in the range of clusters that will be generated. For example, if the minimum number of clusters is 5, and the maximum number of clusters is 7, then 3 interpretations are produced, namely one with 5 classes, one with 6 classes and one with 7 classes.

  4. Maximum iterations – Maximum number of iterations to use when generating a solution.

  5. Terminate if relative change is less than – Threshold for termination.

  6. Repeated runs – Run the algorithm a number of times to ensure robustness with regards to the initial guess.

  7. Constrain cluster shape - 0 is unconstrained, 1 is spherical.

  8. Fuzziness exponent – the degree of fuzziness in the membership of a sample. It can be any number between 1 and infinity but is typically between 1 and 2.

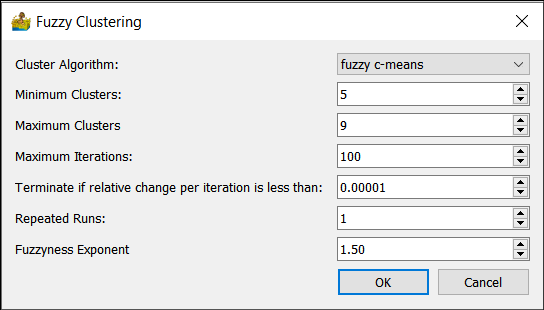
_images/clustfuzzy.png

Fuzzy Clustering options.#

References#

Paasche, H., Eberle, D.G. 2009. Rapid integration of large airborne geophysical data suites using a fuzzy partitioning cluster algorithm: a tool for geological mapping and mineral exploration targeting. Exploration Geophysics, 40, 277-287.

Paasche, H. and Eberle, D. 2011. Automated compilation of pseudo-lithology maps from geophysical data sets: A comparison of Gustafson-Kessel and fuzzy c-means cluster algorithms. Exploration Geophysics, 42, 275–285, https://doi.org/10.1071/EG11014.

Contents