Gradients

Contents

Gradients#

The gradient calculation calculates different derivatives of the data. It allows for the calculation of a conventional horizontal derivative, a derivative ratio (ratio of x and y derivatives), a vertical derivative and a total horizontal gradient. The algorithms are based on Cooper and Cowan (2006, 2007). The input dataset must be in a projection, not in geographic/geodetic coordinates.

Based on the selected filter, different options become available:

  1. Directional derivative: Calculate a horizontal derivative in the direction of the specified Azimuth, with 0° being E-W, 45° being NW-SE, 90° being N-S and -45° being NE-SW. Features perpendicular to the azimuth are highlighted.

  2. Derivative Ratio: Calculate the ratio of x and y derivatives using the following equation (Cooper and Cowan, 2007)

\[DR=tan^{-1}\left({\frac{\frac{df}{dx}} {\mid{\frac{df}{dy}} \mid ^{n}}}\right)\]

where n is the Strength Factor that controls the strength of the filter. A value of 1 is recommended as a starting point. The Azimuth works the same way as for the Directional Derivative.

  1. Vertical Derivative: Calculates the first vertical derivative of a data set.

  2. Total Horizontal Gradient: Combines the horizontal derivatives to enhance features of any orientation (Cooper and Cowan, 2006).

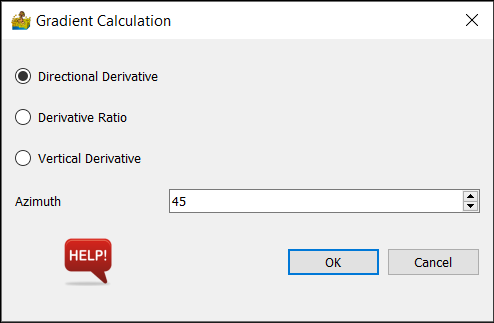
_images/rastergrad.png

Gradient calculation options.#

References#

Cooper, G.R.J. and Cowan, D.R. 2006. Enhancing potential field data using filters based on the local phase. Computers and Geosciences, 32, 1585–1591, https://doi.org/10.1016/j.cageo.2006.02.016.

Cooper,G.R.J., Cowan, D.R. 2007. Enhancing linear features in image data using horizontal orthogonal gradient ratios. Computers and Geosciences, 33, p.981-984

Contents